Закон Моргана является одной из основных концепций генетики и имеет большое значение для понимания наследственности. Этот закон был сформулирован американским генетиком Томасом Хант Морганом в начале 20 века. Он является одним из ключевых принципов, которые объясняют, как наследуются различные признаки от родителей к потомкам.
Основная идея закона Моргана заключается в том, что гены находятся на хромосомах и передаются по наследству от одного поколения к другому. Хромосомы расположены парами, и каждая пара состоит из двух одинаковых хромосом, называемых гомологичными хромосомами. На каждой гомологичной хромосоме находятся гены, которые определяют различные наследственные признаки.
Закон Моргана также формулирует правило скрещивания и распределения генов в процессе мейоза. Согласно этому закону, гены находятся на хромосомах в таком порядке, что они передаются вместе во время скрещивания. Однако, ت الинтерфазе хромосомы могут подвергаться перекомбинации, и гены могут перемещаться с одной хромосомы на другую, что приводит к новым комбинациям генов у потомков.
Что такое Закон Моргана?
Закон Моргана был назван в честь американского генетика Томаса Ханта Моргана, который в начале XX века проводил исследования на мухах дрозофилла и впервые предложил это правило.
Согласно Закону Моргана, гены находятся на хромосомах и располагаются на них в определенном порядке. Во время процесса мейоза, при котором происходит образование гамет (половых клеток), хромосомы случайным образом комбинируются и распределяются в потомстве.
Закон Моргана показывает, что связанные гены, расположенные на одной хромосоме, наследуются вместе чаще всего, но иногда между ними может происходить рекомбинация, когда они перемешиваются и наследуются независимо друг от друга.
Закон Моргана имел огромное значение для развития генетики и помог понять, как наследуются различные признаки у организмов.
Определение и история
Закон Моргана был сформулирован американским генетиком Томасом Хант Морганом в начале XX века. В своих экспериментах с мухой Дрозофилой Морган обнаружил ряд отклонений от ожидаемого наследования и предложил данное объяснение. Этот закон имел важное значение для развития генетики, так как предоставил первое объяснение наблюдаемых аномалий в наследовании генов.
Закон Моргана играет важную роль в понимании механизма и наследования генов, а также в прогнозировании наличия или отсутствия определенных генетических заболеваний у потомства. Он также применяется в селекционной работе при искусственном скрещивании животных и растений.
Основные принципы Закона Моргана
Главные принципы Закона Моргана:
- Инвертирующая логика: Закон Моргана утверждает, что инвертированная функция какого-либо логического выражения эквивалентнаусловию отрицания данного выражения, а именно, если «истина» заменить на «ложь» и наоборот, то результат будет такой же.
- Совершенство поставки: В законе Моргана нет указаний о том, на что применяется данное выражение и какие значения оно принимает. Важно лишь соблюдение основных принципов, которые могут использоваться в различных областях и задачах.
- Применимость к различным схемам: Закон Моргана может применяться при проектировании и анализе электронных схем, таких как схемы логических элементов, схемы управления и другие. Это значит, что он не ограничивается конкретными областями применения.
Закон Моргана является основополагающим принципом в цифровой логике и широко применяется в различных областях, связанных с электроникой и компьютерными технологиями.
Применение Закона Моргана
Применение Закона Моргана особенно полезно при работе с логическими операциями NOT, AND и OR.
Суть Закона Моргана заключается в следующем:
- 1. Замена операции NOT перед группой переменных на операцию NOT перед каждой переменной.
- 2. Замена операции AND на операцию OR и наоборот, а также изменение операции NOT, если она предшествует операции AND или OR.
Применение Закона Моргана позволяет упростить логические выражения, делая их более понятными и компактными. Например:
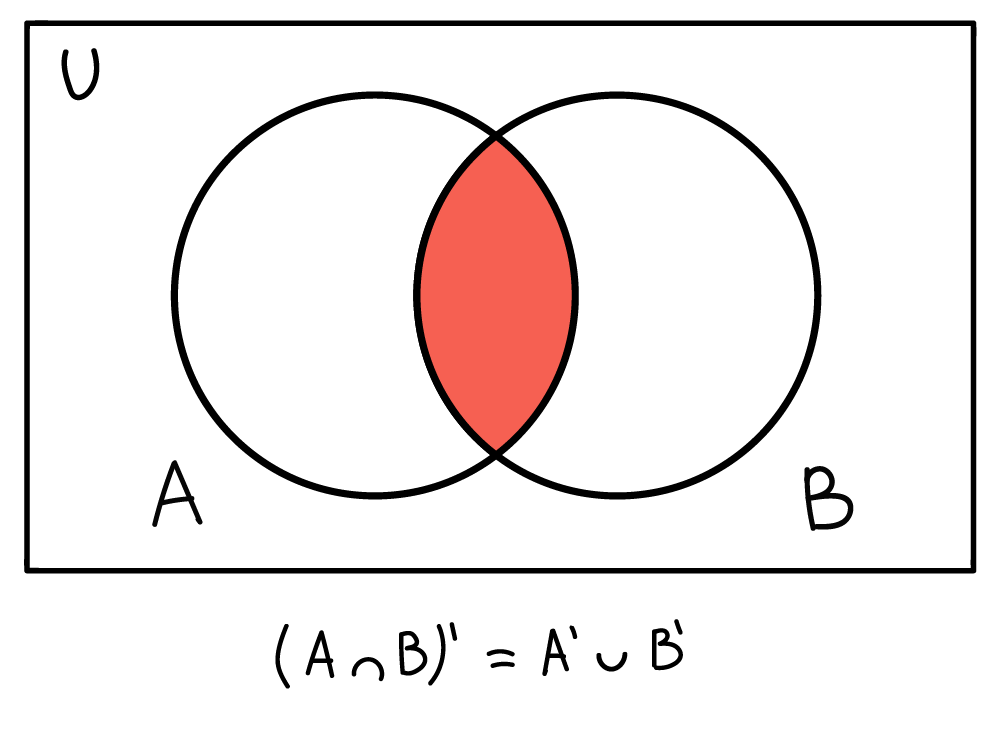
Выражение: NOT (A AND B) можно заменить на NOT A OR NOT B.
Выражение: NOT (A OR B) можно заменить на NOT A AND NOT B.
Также, Закон Моргана можно применять для упрощения выражений с большим количеством переменных и операций. Он позволяет с легкостью преобразовывать сложные выражения в более простые формы.
Важно помнить, что Закон Моргана можно использовать только в контексте операций NOT, AND и OR. Он не применим к другим логическим операциям, таким как XOR, импликация или эквивалентность.
Применение Закона Моргана является неотъемлемой частью работы с логическими выражениями. Он помогает упростить их форму и облегчить понимание логических операций.
Научные исследования
Закон Моргана был формулирован на основе множественных научных исследований, проведенных американским генетиком Томасом Хантом Морганом в начале XX века. Этот закон был открыт при изучении наследования генов у мух Дрозофилы.
Морган провел множество скрещиваний мух, чтобы понять, как наследуются различные признаки. Он обнаружил, что некоторые гены наследуются связанными, то есть передаются вместе при скрещивании, тогда как другие гены наследуются независимо. Этот результат исследования привел Моргана к формулировке Закона Моргана.
Научные исследования, проведенные после открытия Закона Моргана, позволили установить, что этот закон справедлив не только для мух Дрозофилы, но и для многих других организмов, в том числе и для человека. Исследователи изучили механизмы связанного наследования генов на молекулярном уровне и получили много новых данных о генетике.
Научные исследования продолжаются и до сих пор, и закон Моргана остается одним из основных принципов генетики. Он помогает ученым лучше понять, как передаются гены от поколения к поколению и как различные гены взаимодействуют друг с другом.
Философские аспекты
Согласно закону Моргана, отрицание конъюнкции двух утверждений эквивалентно дизъюнкции отрицаний этих утверждений. Упрощенно говоря, в контексте философии это означает, что для опровержения объединения двух истинных утверждений достаточно опровергнуть любое из них.
Пусть у нас есть два утверждения: «A» и «B». Согласно закону Моргана, если оба утверждения истинны, то их конъюнкция «A AND B» также будет истинной. Следовательно, чтобы опровергнуть это объединение, необходимо, чтобы хотя бы одно из утверждений было ложным.
Философский аспект закона Моргана заключается в установлении взаимосвязи между логикой и принципами объективной реальности. Он позволяет нам логически обосновывать истинность или ложность утверждений на основе их взаимоотношений. Это особенно важно в философии, где мы стремимся к поиску истины и пониманию мира вокруг нас.
Примеры из практики
Закон Моргана широко используется в логике и алгебре булевых функций. Рассмотрим несколько примеров, чтобы лучше понять его суть.
Пример 1: Даны две булевы функции: A = NOT(A AND B) и B = NOT(B OR C). Найдем функцию, равную NOT(A OR B).
Сначала применим закон Моргана к функции A: NOT(A AND B) = NOT A OR NOT B.
Затем применим закон Моргана к функции B: NOT(B OR C) = NOT B AND NOT C.
Теперь можем выразить NOT(A OR B) с помощью уже упрощенных функций: NOT(A OR B) = NOT (NOT A AND NOT B) = NOT NOT A OR NOT NOT B = A OR B.
Пример 2: Предположим, что мы имеем 2 множества A и B. Найдем дополнение объединения множеств A и B.
Дополнение объединения множеств A и B можно рассматривать как пересечение их дополнений, и применить закон Моргана.
Дополнение объединения множеств можно записать следующим образом: NOT(A U B) = NOT A ∩ NOT B.
Примечание: U — символ для обозначения объединения, а ∩ — символ для обозначения пересечения.
Используя закон Моргана, мы можем выразить дополнение объединения множеств A и B через пересечение их дополнений: NOT(A U B) = NOT A ∩ NOT B.
Пример 3: Рассмотрим следующую булеву функцию: F = (A AND B) OR (C AND D).
Применим закон Моргана к этой функции: NOT((A AND B) OR (C AND D)) = NOT(A AND B) AND NOT(C AND D).
Далее, с помощью закона дистрибутивности, можно упростить NOT(A AND B) AND NOT(C AND D) следующим образом:
NOT(A AND B) AND NOT(C AND D) = (NOT A OR NOT B) AND (NOT C OR NOT D).
Таким образом, мы получили упрощенную форму булевой функции F с применением закона Моргана и закона дистрибутивности.
Суть закона Моргана заключается в следующем:
1. Отрицание конъюнкции (логического И) равно дизъюнкции (логическому ИЛИ) отрицаний.
2. Отрицание дизъюнкции (логического ИЛИ) равно конъюнкции (логическому И) отрицаний.
Этот закон позволяет заменить сложные выражения более простыми и удобными для дальнейших вычислений. Он также помогает в анализе и упрощении логических утверждений.
Закон Моргана находит применение в различных областях, таких как математика, логика, электротехника и программирование. Понимание этого закона позволяет более эффективно решать задачи и выполнять логические операции.
Обязательное знание закона Моргана может быть полезным для всех, кто работает с алгеброй, логикой или выполняет операции подобные логическим в различных областях научных и технических исследований.
Подводя итог, можно сказать, что закон Моргана является мощным инструментом, который позволяет упростить алгебраические и логические выражения, а также анализировать их с использованием простых правил и операций.
Вопрос-ответ:
Как называется закон, который рассматривается в статье?
Закон Моргана.
Какую суть имеет Закон Моргана?
Суть закона Моргана сводится к определению отрицания логических операций или выражений.
Можете подробнее рассказать о Законе Моргана?
Закон Моргана это логическое правило, которое позволяет менять логические операции (конъюнкцию и дизъюнкцию) на их отрицания. Например, вместо «не пила и не ела» можно сказать «не пила или не ела».
Как применяется Закон Моргана в логике?
В логике Закон Моргана используется для упрощения и перестановки логических выражений. Он помогает упростить сложные формулы и сделать их более понятными.
Какие еще примеры можно привести для Закона Моргана?
Примеры применения Закона Моргана включают в себя сокращение двойного отрицания, перестановку местами операций «и» и «или», а также отрицание конъюнкции и дизъюнкции.
Как называется закон об операциях с логическими выражениями?
Закон Моргана.
В чем суть закона Моргана?
Суть закона Моргана заключается в том, что отрицание конъюнкции (логического «И») эквивалентно дизъюнкции (логическому «ИЛИ») отрицаний, и отрицание дизъюнкции эквивалентно конъюнкции отрицаний.